Une boucle non bornée permet de répéter des instructions
tant qu'un test logique renvoie la valeur "vrai".
On parle de boucle non bornée car le nombre d'itérations
effectué n'est pas fixé à l'avance.
Dans l'illustration ci-dessous, on lance un dé tant que le 4 n'est pas sorti.
On utilise le mot-clé "while" pour introduire une
boucle non bornée, vient ensuite le test logique.
La première ligne se termine par deux points ":".
Le bloc d'instructions à exécuter tant que le test
renvoie la valeur "True" est indenté. On quitte ce
bloc lorsque le test logique renvoie "False".

Le programme ci-dessous permet de lancer un dé tant que le 4 n'est pas sortie.
Une fois le 4 sorti, la fonction attente() renvoie le nombre de lancers nécessaires.
★ Lire ce programme et identifier la syntaxe de la boucle bornée.
★ Exécuter le programme, puis appeler attente( ) plusieurs fois dans la console.
La superficie occupée par une colonie de bactéries double chaque jour, l'aire initiale est de 3 cm². La fonction seuil( ) renvoie le nombre de jours entiers nécessaires pour que l'aire dépasse 90 cm² ainsi que l'aire atteinte.
★ Exécuter le programme, puis appeler la fonction seuil( ) dans la console.
La fonction temps( ) définie ci-dessous, prend un capital initial et un taux. Elle renvoie le nombre d'années nécessaires pour au moins doubler le capital initial.
★ Exécuter le programme ci-dessus, puis, appeler temps(1000, 0.05).
La séquence de Syracuse associée à un entier n > 1 est obtenue en appliquant l'alorithme ci-dessous. Vérifier mentalement que pour n = 5, on obtient la séquence 5, 16, 8, 4, 2, 1.
On a traduit l'algorithme en langage python. La fonction syracuse(n) ci-dessous renvoie la séquence associée à l'entier n pris en paramètre.
★ Observer la structure du programme et remarquer les indentations successives.
★ Exécuter le programme ci-dessus, puis, appeler syracuse(n) pour différentes valeurs du paramètre n.
Chaque année, les surfaces agricoles d'une commune sont réduites de moitié.
En 2021 la surface agricole totale était de 230 ha. On souhaite déterminer
dans combien d'années cette surface passera en dessous de 15 ha.
La fonction définie ci-dessous renvoie ce nombre ainsi que l'aire atteinte.
★ Compléter la ligne 4, puis exécuter le programme.
★ Appeler la fonction surface( ).

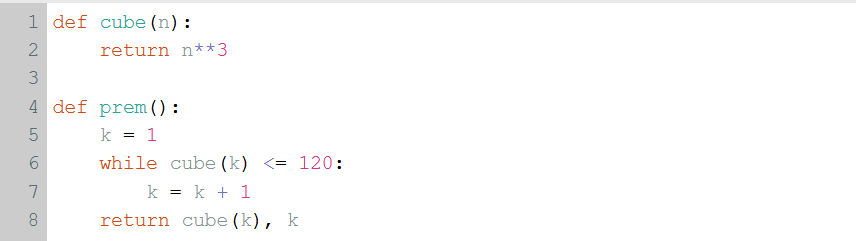
On souhaite déterminer le premier entier naturel dont le cube est supérieur à 120.
Completer la ligne 6 du programme en utisisant la fonction cube.
Après avoir exécuté le programme, appeler la fonction prem().
Un appartement coûte aujourd'hui 230 000 euros. On prévoit une hausse régulière de son prix de 3 % par an.
★ Définir une la fonction nbr(cible) qui prend en paramètre un prix "cible" et renvoie le nombre d'années
entières nécessaires pour atteindre ce prix, par exemple, nbr(300000) doit renvoyer le nombre d'années nécessaires pour que le prix
de l'appartement atteigne au moins 300 000 euros.
★ Exécuter votre programme, puis appeler nbr(cible), pour
différentes valeurs du paramètre cible.
