Syntaxe
Dans la boucle ci-dessous, la variable k parcourt de gauche à droite chacun des
trois éléments de l'ensemble ordonné (0, 1, 2)
Pour chaque valeur de k, le bloc d'instructions après l'indentation est exécuté.
★ Lire ce programme.
★ Prédire l'affichage obtenu.
★ Exécuter le programme.
Remarque
La fonction range() permet de simplifier l'écriture des boucles parcourant des ensembles de nombres entiers.
★ range(5) permet de parcourir l'ensemble (0, 1, 2, 3, 4).
Attention! La dernière valeur est 4 et non 5.
★ range(3, 8) permet de parcourir l'ensemble (3, 4, 5, 6, 7)
★ range(1, 11, 3) permet de parcourir les entiers de 1 à 10 en faisant des pas de 3, Cela
correspond à l'ensemble (1, 4, 7, 10)
Comme le montrent les exemples ci-dessous, la variable associée à la boucle "for"
peut parcourir des ensembles de nombres entiers ou des chaines de caractères.
Exemples
Exemple 1
Dans le programme ci-dessous, l'appel triangle(4) renvoie le nombre triangulaire T4.T4 correspond à la somme des entiers de 1 à 4.
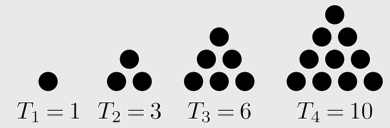
★ Exécuter le programme, puis appeler triangle(3) dans la console.
★ Décomposer mentalement les étapes permettant d'obtenir triangle(3).
Exemple 2
L'exemple suivant présente une boucle parcourant une chaine de caractères.
★ Exécuter le programme ci-dessus, puis, appeler inverse("soleil"),
inverse("kayak") ...
Ne pas oubiler les guillements car nous travaillons avec des chaines de caractères.
Exemple 3
L'appel listebis(a, b) renvoie la liste des années bissextiles entre les années a et b.
★ Exécuter le programme ci-dessus, puis, appeler listebis(1979, 2022).
Exemple 4
Dans cet exemple, la variable couleur de la boucle parcourt la liste:
couleurs = ['red', 'orange', 'yellow', 'lightgreen', 'lightblue', 'violet']
★ Exécuter le programme puis, analyser les lignes 4, 8 et 9.
Exercices
Exercice 1
★ Lire puis exécuter le programme ci-dessous.
★ Appeler f( ), puis g( ).
★ Expliquer la différence des affichages obtenus.
Dans la définition de la fonction f, l'instruction d'affichage est incluse
dans le bloc indenté, elle est donc répétée à chaque passage dans la boucle.
Par contre, pour la fonction g, l'instruction en ligne 11 n'est pas dans le bloc
indenté, l'affichage est donc effectué une seule fois après la sortie de la boucle.
Exercice 2
★ Modifier le programme ci-dessous pour obtenir un carré.

Exercice 3
La fonction div ci-dessous prend un entier n en paramètre et renvoie la liste de ses diviseurs.
★ Quel est l'ensemble de nombres parcouru par range(1, n) ?
★ Modifier la ligne 3 pour que la boucle parcourt l'ensemble nécessaire.
★ Ajouter le code manquant à la ligne 4 en prenant garde à l'indentation.
Après avoir exécuté le programme, appeler plusieurs fois la fonction
div pour différentes valeurs de n .

Exercice 4
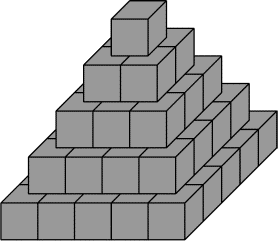
★ Compléter la fonction "vol" qui prend
le nombre d'étages en paramètre et renvoie le nombre de cubes nécessaires pour réaliser cette pyramide.
★ Exécuter votre programme, puis appeler vol(2), puis vol(10).

Digression numérique
Comment les ordinateurs simulent-ils le hasard ?

Les ordinateurs ne sont pas en mesure de produire des séries de nombres aléatoires.
On produit pour approcher le hasard des séries de nombres pseudo-aléatoires générés
grâce à des outils mathématiques.
Le programme ci-dessous reproduit le générateur de Marsaglia utilisé sur l'ordinateur VAX11 dans les années 70.
Ce générateur à congruence linéaire repose sur la suite récurrente :
Xn+1 = 69069 × Xn modulo 232 avec X0 = 13.
Ce générateur permet d'obtenir une longue liste de nombres pseudo-aléatoires, la séquence ne se répète qu'au bout
de 232 nombres.
En exécutant le programme ci-dessous, on génère la liste des 6 premiers nombres pseudo-aléatoires correspondant à une graine de 13.
Remarque
Une fois la graine choisie, les séries obtenues sont déterminées et donc prévisibles. La fonction seed du module random permet de changer la graine du générateur. Si les élèves d'une classe saisissent tous seed(13) après avoir importé le module random, la séquence des nombres pseudo-aléatoires générés sera identique pour tous. (Ceci n'est pas très aléatoire mais peut-être pratique en TP).